Fundamentals
Naming Requirements of Functions
These are keywords; reversed words.
case class data default deriving
do else foreign if import in
infix infixl infixr instance let
module newtype of then type where
Standard Prelude
main = do
let x = [1, 2, 3, 4, 5]
print (head x) -- 1
print (tail x) -- [2, 3, 4, 5]
print (init x) -- [1, 2, 3, 4]
print (last x) -- 5
print (x !! 2) -- 3
print (take 3 x) -- [1, 2, 3]
print (drop 3 x) -- [4, 5]
print (length x) -- 5
print (sum x) -- 15
print (product x) -- 120
print ([1, 2, 3] ++ [4, 5]) -- [1 , 2, 3, 4, 5]
print (reverse x) -- [5, 4, 3, 2, 1]
Types
A type is a collection of related values.
Notation 1
v :: T means e is a value in the type T.
False :: Bool
True :: Bool
not :: Bool -> Bool
Notation 2
e :: T means evaluation of the expression e will produce a value of type T.
not False :: Bool
not True :: Bool
not (not False) :: Bool
Typing rule
f :: A -> B e :: A
-------------------
f e -> B
Type Interface and Type Safe
type interface that evaluates types under typing rule.
type interface precedes evaluation of values so Haskell programs are type safe.
Basic Types
| types | description |
|---|---|
| Bool | |
| Char | |
| String | |
| Int | fixed-precision intergers. the range is |
| Integer | arbitarary-precision integers |
| Float | single-precision floating-point numbers |
| Double | double-precision floating-point numbers |
List Types
[['a', 'b'], ['c', 'd', 'e']] :: [[Char]]
Tuple Types
arity: the number of components in a tuple
- arity zero:
(); the empty tuple - arity one: Not Permitted
- arity two: pairs
- arity three: triples
tp1 = ("Yes", True, 'a') :: (String, Bool, Char)
tp2 = (3, "Blue") :: (Int, String)
main = do
print (fst tpl) -- 3
print (snd tpl) -- "Blue"
Function Types
A function is mapping from arguments of one type to results of another type.
add :: (Int, Int) -> Int
add (x, y) = x + y
add (1, 2) -- 3
zeroto :: Int -> [Int]
zeroto n = [0..n]
Curried Functions
add' :: Int -> (Int -> Int)
add' x y = x + y
add' 1 2 -- 3
mult :: Int -> (Int -> (Int -> Int))
mult x y z = x * y * z
Don't confuse currying and partial application
- Currying: divide a function into functions with only one argument and nest them.
- Partial Application: create a new function by fixing partial arguments of a original function
-- currying
add' :: Int -> (Int - > Int)
add' x y = x + y
add' 1 2
-- partial application 1
add'' = add' 1
add'' 2 -- 3
-- partial application 2
add'' y = add (1, y)
add'' 2 -- 3
Polymorphic Types
fst :: (a, b) -> a
head :: [a] -> a
take :: Int -> [a] -> [a]
zip :: [a] -> [b] -> [(a, b)]
id :: a -> a
Type Variable
must begin with a lower-case letter
length :: [a] -> Int
Overloaded Types
contains one or more class constraints
(+) :: Num a => a -> a -> a
negate :: Num a => a -> a
abs :: Num a => a -> a
Class Constraint
-- C: class name
-- a: type variable (an assined type to `a` is called `instance` of class `C`)
C a
Classes
A class is a collection of types that support certain overloaded operatoins; methods (e.g. (==), (/=) in Eq)
Eq - equality types
(==) :: a -> a -> Bool
(/=) :: a -> a -> Bool
All the basic types Bool, Char, String, Int, Integer, Float and Double are instances of the Eq class.
As are list and tuple types, provided that element and component types of the basic types are instances.
Ord - ordered types
(<) :: a -> a -> Bool
(<=) :: a -> a -> Bool
(>) :: a -> a -> Bool
(>=) :: a -> a -> Bool
min :: a -> a -> a
max :: a -> a -> a
Show - showable types
show :: a -> String
Read - readable types
read :: String -> a
Num - numeric types
(+) :: a -> a -> a
(-) :: a -> a -> a
(*) :: a -> a -> a
negate :: a -> a
abs :: a -> a signum :: a -> a
Integral - integral types
Types to support the methods of integer division and integer remainder. Int and Integer are instances of Integral.
div :: a -> a -> a
mod :: a -> a -> a
Fractional - fractional types
support the methods of fractional division and fractinal reciprocation
(/) :: a -> a -> a
recip :: a -> a
> 7.0 / 2.0
3.5
> recip 2.0
0.5
Definning Functions
Conditional Expressions
abs :: Int -> Int
abs n = if n >= 0 then n else -n
signum :: Int -> Int
signum n = if n < 0 then -1 else
if n == 0 then 0 else 1
Guarded Equations
abs n
| n >= 0 = n
| otherwise = - n
signum n
| n < 0 = -1
| n == 0 = 0
| otherwise = 1
The symbol | is read as such that.
Pattern matching
not :: Bool -> Bool
not False = True
not True = False
(&&) :: Bool -> Bool -> Bool
True && True = True
_ && _ = False
Tuple Patterns
fst :: (a, b) -> a
fst (x, _) = x
snd :: (a, b) -> b
snd (_, y) = y
List Patterns
matches any list of the same length whose elements all match the corresponding patterns in order.
test :: [Char] -> Bool
test ['a', _, _] = True
test _ = False
cons operator : prepends a new element to an existing list.
[1, 2, 3]
= 1:[2, 3]
= 1:(2:[3])
= 1:(2:(3:[]))
test :: [Char] -> Bool
test ('a':_) = True
test _ = False
head :: [a] -> a
head (x:_) = x
tail :: [a] -> [a]
tail (_:xs) = xs
Lambda Expressions
\x -> x + x
> (\x -> x + x) 2
4
add :: Int -> Int -> Int
add x y = x + y
add = \x -> (\y -> x + y)
const :: a -> b -> a
const x _ = x
const x = \_ -> x
odds :: Int -> [Int]
odds n = map f [0..n-1]
where f x = x * 2 + 1
odds n = map (\x -> x * 2 + 1) [0..n-1]
Operator Sections
- operators: functions with two arguments
- sections: operators formed as
(#),(x #), or so
(#) = \x -> (\y -> x # y)
(x #) = \y -> x # y
(# y) = \x -> x # y
List Comprehensions
xs = [x^2 | x <- [1..5]] -- [1, 4, 9, 16, 25]
|: such that<-: drawn fromx <- [1..5]: generator
xs2 = [(x, y) | x <- [1, 2, 3,], y <- [4, 5]]
-- [(1, 4), (1, 5), (2, 4), (2, 5), (3, 4), (3, 5)]
xs3 = [(x, y) | y <- [4, 5], x <- [1, 2, 3]]
-- [(1, 4), (2, 4), (3, 4), (1, 5), (2, 5), (3, 5)]
xs4 = [(x, y) | x <- [1..3], y <- [x..3]]
-- [(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)]
concat :: [[a]] -> [a]
concat xss = [x | xs <- xss, x <- xs]
firsts :: [(a, b)] -> [a]
firsts ps = [x | (x, _) <- ps]
length :: [a] -> Int
length xs = sum [1 | _ <- xs]
main = do
print (concat [[1, 2, 3], [4, 5, 6]]) -- [1,2,3,4,5,6]
print ([1, 2, 3] ++ [4, 5, 6]) -- [1,2,3,4,5,6]
print (firsts [(1, 2), (3, 4), (5, 6)]) -- [1, 3, 5]
print (length [1, 2, 3]) -- 3
Guard
expressions to filter generated values
evens :: Integral a => a -> [a]
evens n = [x | x <- [0 .. n], even x]
factors :: Integral a => a -> [a]
factors n = [x | x <- [1 .. n], n `mod` x == 0]
prime :: Integral a => a -> Bool
prime n = factors n == [1, n]
{- Note:
Deciding that a number is prime does not require
the `prime` to produce all of its factors,
because under lazy evaluation the result `False` is returned
as soon as any factor other than one or the number itself is produced.
e.g. `prime 15` returns `False` when 3 in its factors `[1, 3, 5, 15]` is produced in `factors`.
-}
primes :: Integral a => a -> [a]
primes n = [x | x <- [2 .. n], prime x]
find :: Eq a1 => a1 -> [(a1, a2)] -> [a2]
find k t = [v | (k', v) <- t, k == k']
main = do
print (evens 10) -- [0,2,4,6,8,10]
print (factors 12) -- [1,2,3,4,6,12]
print (prime 15) -- False
print (prime 7) -- True
print (primes 40) -- [2,3,5,7,11,13,17,19,23,29,31,37]
print (find 'b' [('a', 1), ('b', 2), ('c', 3), ('b', 4)]) -- [2, 4]
zip function
pairs :: [b] -> [(b, b)]
pairs xs = zip xs (tail xs)
sorted :: Ord a => [a] -> Bool
sorted xs = and [x <= y | (x, y) <- pairs xs]
positions :: (Num a1, Enum a1, Eq a2) => a2 -> [a2] -> [a1]
positions x xs = [i | (x', i) <- zip xs [0 ..], x == x']
main = do
print (zip ['a', 'b', 'c'] [1, 2, 3, 4]) -- [('a',1),('b',2),('c',3)]
print (pairs [1, 2, 3, 4]) -- [(1,2),(2,3),(3,4)]
print (sorted [1, 2, 3, 4]) -- True
print (sorted [1, 3, 2, 4]) -- False
print (positions False [True, False, True, False]) -- [1, 3]
String comprehensions
String is a list of Char
lowers :: [Char] -> Int
lowers xs = length [x | x <- xs, x >= 'a' && x <= 'z']
count :: Eq a => a -> [a] -> Int
count x xs = length [x' | x' <- xs, x == x']
main = do
print ("abcde" !! 2) -- 'c'
print (take 3 "abcde") -- "abc"
print (length "abcde") -- 5
print (zip "abc" [1, 2, 3, 4]) -- [('a',1),('b',2),('c',3)]
print (lowers "Haskell") -- 6
print (count 's' "Mississippi") -- 4
Recursive Functions
fac :: Int -> Int
fac 0 = 1
fac n = n * fac (n - 1)
(*) :: Int -> Int -> Int
m * 0 = 0
m * n = m + (m * (n - 1))
Recursion on Lists
product :: Num a => [a] -> a
product [] = 1
product (n:ns) = n * product ns
length :: [a] -> Int
length [] = 1
length (_:xs) = 1 + length xs
reverse :: [a] -> a
reverse [] = []
reverse (x:xs) = reverse xs ++ [x]
(++) :: [a] -> [a] -> [a]
[] ++ ys = ys
(x:xs) ++ ys = x:(xs ++ ys)
insert :: Ord a => a -> [a] -> [a]
insert x [] = [x]
insert x (y:ys)
| x <= y = x:y:ys
| otherwise = y:insert x ys
-- insertion sort
isort :: Ord a => [a] -> [a]
isort [] = []
isort (x:xs) = insert x (isort xs)
Multiple Arguments
zip :: [a] -> [a] -> [(a, b)]
zip [] _ = []
zip _ [] = []
zip (x:xs) (y:ys) = (x, y):zip xs ys
drop :: Int -> [a] -> [a]
drop 0 xs = xs
drop _ [] = []
drop n (x:xs) = drop (n - 1) xs
Multiple Recursion
fib :: Int -> Int
fib 0 = 0
fib 1= 1
fib n = fib (n - 2) + fib (n - 1)
qsort :: Ord a => [a] -> [a]
qsort [] = []
qsort (x:xs) = qsort smaller ++ [x] ++ qsort larger
where
smaller = [a | a <- xs, a <= x]
larger = [b | b <- xs, b > x]
Mutual Recursion
even :: Int -> Bool
even 0 = True
even n = odd (n - 1)
odd :: Int -> Bool
odd 0 = False
odd n = even (n - 1)
evens :: [a] -> [a]
evens [] = []
evens (x:xs) = x:odds xs
odds :: [a] -> [a]
odds [] = []
odds (_:xs) = evens xs
Generalizing and Simplifying
-- before
product :: Num a => [a] -> a
product [] = 1
product (n:ns) = n * product ns
-- after
product :: Num a => [a] -> a
product = foldr (*) 1
-- before
init :: [a] -> [a]
init (x:xs)
| null xs = []
| otherwise = x:init xs
-- after
init :: [a] -> [a]
init [_] = []
init (x:xs) = x:init xs
Higher-Order Functions
Functions that take a function as an argument or return a function as a result
Processing Lists
-- list conprehension ver.
map :: (a -> b) -> [a] -> [b]
map f xs = [f x | x <- xs]
-- recursive ver.
map :: (a -> b) -> [a] -> [b]
map f [] = []
map f (x : xs) = f x : map f xs
-- list conprehension ver.
filter :: (a -> Bool) -> [a] -> [a]
filter p xs = [x | x <- xs, p x]
-- recursive ver.
filter :: (a -> Bool) -> [a] -> [a]
filter p [] = []
filter p (x : xs)
| p x = x : filter p xs
| otherwise = filter p xs
main = do
print (all even [2, 4, 6, 8]) -- True
print (any odd [2, 4, 6, 8]) -- False
print (takeWhile even [2, 4, 6, 7, 8]) -- [2, 4, 6]
print (dropWhile odd [1, 3, 5, 6, 7]) -- [6, 7]
foldr()
foldr (#) v [x0, x1, ..., xn] = x0 # (x1 # (... (xn # v)))
f v
-- recursive ver.
foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f v [] = v
foldr f v (x : xs) = f x (foldr f v xs)
sum :: Num a => [a] -> a
-- sum [] = 0
-- sum (x : xs) = x + sum(xs)
sum = foldr (+) 0
product :: Num a => [a] -> a
product = foldr (*) 1
or :: [Bool] -> Bool
or = foldr (||) False
and :: [Bool] -> Bool
and = foldr (&&) True
length :: [a] -> Int
-- length [] = 0
-- length (_:xs) = 1 + length xs
length = foldr (\_ n -> 1 + n) 0
-- snoc is `cons` backwards
snoc :: a -> [a] -> [a]
snoc x xs = xs ++ [x]
reverse :: [a] -> [a]
-- reverse [] = []
-- reverse (x : xs) = reverse xs ++ [x]
reverse :: [a] -> [a]
reverse = foldr snoc []
foldl()
v is accumlator.
foldl (#) v [x0, x1, ..., xn] = (((v # x0) # x1)...) # xn
-- recursive ver.
foldl :: (a -> b -> a) -> a -> [b] -> a
foldl f v [] = v
fold f v (x : xs) = foldl f (v + x) xs
sum' :: Num a => [a] -> a
sum' = sum'' 0
where
sum'' v [] = v
sum'' v (x : xs) = sum'' (v + x) xs
sum :: Num a => [a] -> a
sum = foldl (+) 0
product :: Num a => [a] -> a
product = foldl (*) 1
or :: [Bool] -> Bool
or = foldl (||) False
and :: [Bool] -> Bool
and = foldr (&&) True
length :: [a] -> Int
length = foldl (\n _ -> n + 1) 0
reverse :: [a] -> [a]
reverse = foldl (\xs x -> x : xs) []
Composition Operator
f . g is read as f composed with g .
(.) :: (b -> c) -> (a -> b) -> (a -> c)
f . g = \x -> f (g x)
-- odd n = not (even n)
odd = not . even
-- twice f x = f (f x)
twice = f . f
-- sumsqreven ns = sum (map (^2) (filter even ns))
sumsqreven = sum . map (^2) . filter even
-- identity function; id.f = f, f.id = f
id :: a -> a
id = \x -> x
compose :: [a -> a] -> (a -> a)
compose = foldr (.) id -- make the composition of a list of functions
-- produces an infinite list
iterate f x = [x, f x, f(f x), f(f(f x)), ...]
iterate (*2) 1 -- [1, 2, 4, 8, ...]
-- repeat :: a -> [a]: procudes an infinite list of copies of a value
repeat 0 -- [0, 0, 0, 0, ...]
take 8 (repeat 0) -- [0, 0, 0, 0, 0, 0, 0, 0] -- lazy evaluation
Type Declarations
type String = [Char]
type Pos = (Int, Int)
type Trans = Pos -> Pos
type Pair a = (a, a)
type Assoc k v = [(k, v)]
find :: Eq k => k -> Assoc k v -> v
find k t = head [v | (k', v) <- t, k == k']
Data Declarations
|is read as or.- constructors new values of the type (e.g.
FalseandTrueare constructors of Bool)
data Bool = False | True
data Move = North | South | East | West
move :: Move -> Pos -> Pos
move North (x, y) = (x, y + 1)
move South (x, y) = (x, y - 1)
move East (x, y) = (x + 1, y)
move West (x, y) = (x - 1, y)
moves :: [Move] -> Pos -> Pos
moves [] p = p
moves (m : ms) p = moves ms (move m p)
Cosntructor Functions
vs. normal functions
- have no defining equations and exist as data
- e.g.
negate 1.0can be evaluated to -1.0 by definition of negateCircle 1.0is already fully evaluated and cannot be further simplified
-- Circle :: Float -> Shape
-- Rect :: Float -> Float -> Shape
data Shape = Circle Float | Rect Float Float
square :: Float -> Shape
square n = Rect n n
area :: Shape -> Float
area (Circle r) = pi * r ^ 2
area (Rect x y) = x * y
type as a argument
data Maybe a = Nothing | Just a
safediv :: Int -> Int -> Maybe Int
safediv _ 0 = Nothing
safediv m n = Just (m `div` n)
safehead :: [a] -> Maybe a
safehead [] = Nothing
safehead xs = Just (head xs)
Newtype Declarations
newtype declarations are to improve type safety without affecting perfomance.
it must have Constructor such as N in below example.
newtype Nat = N Int
type Nat = Int
data Nat = N Int
vs. type
- Using newtype rather than type means that
NatandIntare different types rather than synonyms - The type system of Haskell ensures that they cannot accidentally be mixed up in programs
vs. data
- Using newtype rather than data brings an efficiency benefit
- newtype constructors such as
Ndo not incur any cost when programs are evaluated, as they are automatically removed by the compiler once type checking is completed
Recursive Types
data Nat = Zero | Succ Nat
nat2int :: Nat -> Int
nat2int Zero = 0
nat2int (Succ n) = 1 + nat2int n
int2nat :: Int -> Nat
int2nat 0 = Zero
int2nat n = Succ (int2nat (n - 1))
add :: Nat -> Nat -> Nat
add m n = int2nat (nat2int m + nat2int n)
add' :: Nat -> Nat -> Nat
add' Zero n = n
add' (Succ m) n = Succ (add' m n)
{- e.g. 2 + 1
add (Succ (Succ Zero)) (Succ Zero)
= (Succ add (Succ Zero) (Succ Zero))
= Succ (Succ (add Zero (Succ Zero)))
= Succ (Succ (Succ Zero))
-}
data Tree a = Leaf a | Node (Tree a) a (Tree a)
t :: Tree Int
t = Node (Node (Leaf 1) 3 (Leaf 4)) 5 (Node (Leaf 6) 7 (Leaf 9))
flatten :: Tree a -> [a]
flatten (Leaf x) = [x]
flatten (Node l x r) = flatten l ++ [x] ++ flatten r
occurs :: Eq a => a -> Tree a -> Bool
occurs x (Leaf y) = x == y
occurs x (Node l y r) = x == y || occurs x l || occurs x r
occurs' :: Ord a => a -> Tree a -> Bool
occurs' x (Leaf y) = x == y
occurs' x (Node l y r)
| x == y = True
| x < y = occurs' x l
| otherwise = occurs' x r
Class and Instance Declarations
- type
ais an instance of the classEq - types of instance must support functions;
(==),(/=) (/=)is defined as default definition, so declaring an instance only requires a definition of(==)
class Eq a where
(==), (/=) :: a -> a -> Bool
x /= y = not (x == y)
instance Eq Bool where
False == False = True
True == True = True
_ == _ = False
- type
ato be instance of classOrdmust be an instance of classEq
class Eq a => Ord a where
(<), (<=), (>), (>=) :: a -> a -> Bool
min, max :: a -> a -> a
min x y
| x <= y = x
| otherwise = y
max x y
| x <= y = y
| otherwise = x
instance Ord Bool where
False < True = True
_ < _ = False
b <= c = (b < c) || (b == c)
b > c = c < b
b >= c = c <= b
Derived Instances
data Bool = False | True -- this order is reflected on False < True
deriving (Eq, Ord, Show, Read)
Interactive Programming
Interactive programs has side effects such as additional inputs and outputs while the program is running.
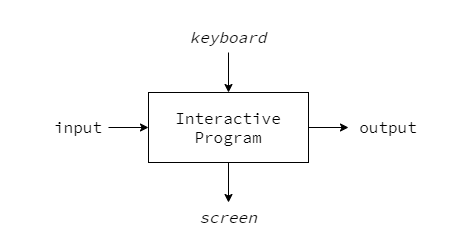
Haskell treats an interactive program as a pure function that takes the current state of world as its arguments, and produces a modified world as its result
Expressions of type IO a are called actions
- type IO Char: type of actions that return a character
- type IO (): type of actions that return the empty tuple
()as a dummy result value
type IO = World -> World
type IO a = World -> (a, World)
type Char -> IO Int -- means type Char -> World -> (Int, World)
Basic Actions
getChar :: IO Char
putChar :: Char -> IO ()
return :: a -> IO a
Sequencing
<-is called generator as with list comprehensions- if a value generated by
aiis unnecessary, generator is abbreviated byaiwhich means_ <- ai
- if a value generated by
do v1 <- a1
v2 <- a2
...
vn <- an
return (f v1 v2 ... vn)
act :: IO (Char, Char)
act = do x <- getChar
getChar
y <- getChar
return (x, y)
Derived primitives
action primitives in the standard prelude
- getLine: read chars until
\n - putStr: without
\n - putStrLn: with
\n
getLine :: IO String
getLine = do x <- getChar
if x == '\n' then
return []
else
do xs <- getLine
return (x : xs)
putStr :: String -> IO ()
putStr [] = return ()
putStr (x : xs) = do putChar x
putCStr xs
putStrLn :: String -> IO ()
putStrLn xs = do putStr xs
putChar '\n'
strlen :: IO ()
strlen = do putStr "Enter a string: "
xs <- getLine
putStr "The string has "
putStr (show (length xs))
putStrLn " characters"
Functors
class of types that support a mapping function.
class Functor f where
fmap :: (a -> b) -> f a -> f b
fmaptakes a function of typea -> band a structure of typef awhose elements have typeafmapapplies the function to each element to give a structure of typef bwhose elements have typeb
instance Functor [] where
-- fmap :: (a -> b) -> [a] -> [b]
fmap = map
instance Functor Maybe where
-- fmap :: (a -> b) -> Maybe a -> Maybe b
fmap _ Nothing = Nothing
fmap g (Just x) = Just (g x)
fmap (+1) Nothing -- Nothing
fmap (*2) (Just 3) -- Just 6
fmap not (Just False) -- Just True
data Tree a = Leaf | Node (Tree a) (Tree a)
deriving Show
instance Functor Tree where
-- fmap :: (a -> b) -> Tree a -> Tree b
fmap g (Leaf x) = Leaf (g x)
fmap g (Node l r) = Node (fmap g l) (fmap g r)
fmap length (Leaf "abc") -- Leaf 3
fmap even (Node (Leaf 1) (Leaf 2)) -- Node (Leaf False) (Leaf True)
instance Functor IO where
-- fmap :: (a -> b) -> IO a -> IO b
fmap g mx = do {x <- mx; return (g x)}
fmap show (return True) -- "True"
inc :: [Int] -> [Int]
inc = map (+ 1)
inc' :: Functor f => f Int -> f Int
inc' = fmap (+ 1)
inc' (Just 1) -- Just 2
inc' [1, 2, 3, 4, 5] -- [2, 3, 4, 5, 6]
inc' (Node (Leaf 1) (Leaf 2)) -- Node (Leaf 2) (Leaf 3)
Functor Laws
fmap id = id
fmap (g . h) = fmap g . fmap h
Applicatives
applicative functors; applicative
the class of functors that support pure and <*> functions
class Functor f => Applicative f where
pure :: a -> f a
(<*>) :: f (a -> b) -> f a -> f b
pure :: a -> f a
(<*>) :: f (a -> b) -> f a -> f b
fmap0 :: a -> f a
fmap0 = pure
fmap1 :: (a -> b) -> f a -> f b
fmap1 = pure g <*> x
fmap2 :: (a -> b -> c) -> f a -> f b -> f c
fmap2 = pure g <*> x <*> y
fmap3 :: (a -> b -> c -> d) -> f a -> f b -> f c -> f d
fmap3 = pure g <*> x <*> y <*> z
...
-- type check. fmap2
-- f (a -> b -> c) -> f a -> f (b -> c)
-- pure g <*> x = x'
-- f (b -> c) -> f b -> f c
-- x' <*> y = res
The applicative style for Maybe supports a form of exceptional programming in which we can apply pure functions to arguments that may fail without the need to manage the propagation of failure ourselves.
instance Applicative Maybe where
-- pure :: a -> Maybe a
pure = Just
-- (<*>) :: Maybe (a -> b) -> Maybe a -> Maybe b
Nothing <*> _ = Nothing
(Just g) <*> mx = fmap g mx
pure (+ 1) <*> Just 1 -- Just 2
pure (+) <*> Just 1 <*> Just 2 -- Just 3
pure (+) <*> Nothing <*> Just 2 -- Nothing
The applicative sytle for lists supports a form of non-deteministic programming in which we can apply pure functions to multi-valued arguments without the need to manage the selection of values or the propagation of failure.
instance Applicative [] where
-- pure :: a -> [a]
pure x = [x]
-- (<*>) :: [a -> b] -> [a] -> [b]
gs <*> xs = [g x | g <- gs, x <- xs]
pure (+ 1) <*> [1, 2, 3] -- [2, 3, 4]
pure (+) <*> [1] <*> [2] -- [3]
pure (*) <*> [1, 2] <*> [3, 4] -- [3, 4, 6, 8]
prods :: [Int] -> [Int] -> [Int]
prods xs ys = [x * y | x <- xs, y <- ys]
prods' :: [Int] -> [Int] -> [Int]
prods' xs ys = pure (*) <*> xs <*> ys
The applicative style for IO supports a form of interactive programming in which we can apply pure functions to impure arguments without the need to manage the sequencing of actions or the extranction of result values.
instance Applicative IO where
-- pure :: a -> IO a
pure = return
-- (<*>) :: IO (a -> b) -> IO a -> IO b
mb <*> mx = do {g <- mg; x <- mx; return (g x)}
getChars :: Int -> IO String
getChars 0 = return []
getChars n = pure (:) <*> getChar <*> getChars (n - 1)
sequenceA :: Applicative f => [f a] -> f [a]
sequenceA [] = pure []
sequenceA (x : xs) = pure (:) <*> x <*> sequecneA xs
getChars :: Int -> IO String
getChars n = sequenceA (replicate n getChar)
Applicative Laws
pure id <*> x = x -- pure is complemented
pure (g x) = pure g <*> pure x -- occurences of pure can be combined into one
x <*> pure y = pure (\g -> g y) <*> x -- the order in which we evaluate the two components doesn't matter
x <*> (y <*> z) = (pure (.) <*> x <*> y) <*> z -- <*> is associative
these laws ensure that below expression is evaluated uniquely.
pure g <*> x1 <*> x2 <*> ... <*> xn
Infix ver.
fmap g x = pure g <*> x
g <$> x = fmap g x
g <$> x1 <*> x2 <*> ... <*> xn
Monads
class Applicative m => Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m b
return = pure
>>= operator
- called bind.
- ensures that such an expression only succeeds if every component in the sequence succeeds
(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
mx >>= f = case mx of
Nothing -> Nothing
Just x -> f x
-- Notation 1
m1 >>= \x1 ->
m2 >>= \x2 ->
...
mn >>= \xn ->
f x1 x2 ... xn
-- Notation 2
do x1 <- m1
x2 <- m2
...
xn <- mn
f x1 x2 ... xn
Monad Laws
return x >>= f = f x -- (return x) >>= f = f x
mx >>= return = mx
(mx >>= f) >>= g = mx >>= (\x -> (f x >>= g)) -- assosiatative
Usecases
applicative style does not fit the pattern of effectful programming such as the function which is the first argument of <*> is not pure function.
- e.g.
safedivis not a pure function because it returnsMaybe Int, notInt
data Expr = Val Int | Div Expr Expr
eval :: Expr -> Int
eval (Val n) = n
eval (Div x y) = eval x `div` eval y
eval (Div (Val 1) (Val 0)) -- *** Exception: divide by zero
safediv :: Int -> Int -> Maybe Int
safediv _ 0 = Nothing
safediv n m = Just (n `div` m)
eval' :: Expr -> Maybe Int
eval' (Val n) = Just n
eval' (Div x y) = case eval x of
Nothing -> Nothing
Just n -> case eval y of
Nothing -> Nothing
Just m -> safediv n m
eval' (Div (Val 1) (Val 0)) -- Nothing
eval' :: Expr -> Maybe Int
eval' (Val n) = pure n
eval' (Div x y) = pure safediv <*> eval x <*> eval y -- type error
apply monad then
instance Monad Maybe where
-- (>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
Nothing >>= _ = Nothing
(Just x) >>= f = f x
data Expr = Val Int | Div Expr Expr
safediv :: Int -> Int -> Maybe Int
safediv _ 0 = Nothing
safediv n m = Just (n `div` m)
-- Notation 1
eval :: Expr -> Maybe Int
eval (Val n) = Just n
eval (Div x y) =
eval x >>= \n ->
eval y >>= \m ->
safediv n m
-- Notation 2
eval' :: Expr -> Maybe Int
eval' (Val n) = Just n
eval' (Div x y) = do
n <- eval' x
m <- eval' y
safediv n m
instance Monad [] where
-- (>>=) :: [a] -> (a -> [b]) -> [b]
xs >>= f = [y | x <- xs, y <- f x]
pairs :: [a] -> [b] -> [(a, b)]
pairs xs ys =
xs >>= \x ->
ys >>= \y ->
return (x, y)
pairs :: [a] -> [b] -> [(a, b)]
pairs xs ys = do
x <- xs
y <- ys
return (x, y)
The State Monad
type State = Int -- state is just an integer value but this can be modified as required
state tronsformer; ST
takes an input state as its argument and produces an ouptut state as its result
type ST = State -> State
type ST a = State -> (a, State) -- returns State with an output of type `a`
type a -> ST b -- type a -> State -> (b, State)
-- takes State with an input of type `a` and returns State with an output of type `b`
we want to make ST into a monad but types declared using the type mechanism cannot be made into instances of classes.
so we need to define it using newtype.
newtype ST a = S (State -> (a, State))
-- removes dummy constructor `S`
app :: ST a -> State -> (a, State)
app (S st) x = st x
instance Functor ST where
-- fmap :: (a -> b) -> ST a -> ST b
fmap g st = S (\s -> let (x, s') = app st s in (g x, s'))
instance Applicative ST where
-- pure :: a -> ST a
pure x = S (\s -> (x, s))
-- (<*>) :: ST (a -> b) -> ST a -> ST b
stf <*> stx =
S
( \s ->
let (f, s') = app stf s
(x, s'') = app stx s'
in (f x, s'')
)
instance Monad ST where
-- (>>=) :: ST a -> (a -> ST b) -> ST b
st >>= f = S (\s -> let (x, s') = app st s in app (f x) s')
Generic Functions
mapM()
-- defined in Control.Monad
mapM :: Monad m => (a -> m b) -> [a] -> m [b]
mapM f [] = return []
mapM f (x : xs) = do
y <- f x
ys <- mapM f xs
return (y : ys)
import Data.Char
conv :: Char -> Maybe Int
conv c
| isDigit c = Just (digitToInt c)
| otherwise = Nothing
mapM conv "1234" -- Just [1, 2, 3, 4]
mapM conv "123a" -- Nothing
filterM()
-- defined in Control.Monad
filterM :: Monad m => (a -> m Bool) -> [a] -> m [a]
filterM p [] = return []
filterM p (x : xs) = do
b <- p x
ys <- filter M p xs
return (if b then x : ys else ys)
filterM (\x -> [True, False]) [1, 2, 3]
-- [[1, 2, 3], [1, 2], [1, 3], [1], [2, 3], [2], [3], []]
join()
join :: Monad m => m (m a) -> m a
join mmx = do
mx <- mmx
x <- mx
return x
join [[1, 2], [3, 4], [5, 6]] -- [1, 2, 3, 4, 5, 6]
join (Just (Just 1)) -- Just 1
join (Just Nothing) -- Nothing
join Nothing -- Nothing
Alternative
class Applicative f => Alternative f where
empty :: f a
(<|>) :: f a -> f a -> f a
Alternative Laws
empty <|> x = x
x <|> empty = x
x <|> (x <|> y) = (x <|> y) <|> z -- associative
Alternative Instances
instance Alternative Maybe where
-- empty :: Maybe a
empty = Nothing
-- (<|>) :: Maybe a -> Maybe a -> Maybe a
Nothing <|> my = my
(Just x) <|> _ = Just x
Monoids
class Monoids a where
mempty :: a
mappend :: a -> a -> a
mconcat :: [a] -> a
mconcat = foldr mappend mempty
Monoid Laws
mempty `mappend` x = x
x `mappend` mempty = x
x `mappend` (y `mappend` z) = (x `mappend` y) `mappend` z
-- using <> operator
mempty <> x = x
x <> mempty = x
x <> (y <> z) = (x <> y) <> z
Data.Monoid
Lists
instance Monoid [a] where
-- mempty :: [a]
mempty = []
-- (<>) :: [a] -> [a] -> [a]
mappend = (++)
Maybe
instance Monoid a => Monoid (Maybe a) where
-- mempty :: Maybe a
mempty = Nothing
-- (<>) :: Maybe a -> Maybe a -> Maybe a
Nothing <> my = my
mx <> Nothing = mx
Just x <> Just y = Just (x <> y)
Sum
newtype Sum a = Sum a
deriving (Eq, Ord, Show, Read)
getSum :: Sum a -> a
getSum (Sum x) = x
instance Num a => Monoid (Sum a) where
-- mempty :: Sum a
mempty = Sum 0
-- (<>) :: Sum a -> Sum a -> Sum a
Sum x <> Sum y = Sum (x + y)
mconcat [Sum 2, Sum 3, Sum 4] -- Sum 9
Product
newtype Product a = Product a
deriving (Eq, Ord, Show, Read)
getProduct :: Product a -> a
getProduct (Product x) = x
instance Num a => Monoid (Product a) where
-- mempty :: Product a
mempty = Product 1
-- (<>) :: Product a -> Product a -> Product a
Product x <> Product y = Product (x * y)
mconcat [Product 2, Product 3, Product 4] -- Product 24
All
mconcat [All True, All True, All True] -- All True
Any
mconcat [Any False, Any False, Any False] -- Any False
Foldables
Note:
minimal complete definition for an instance of the Foldable class is to define either foldMap or foldr
class Foldable t where
fold :: Monoid a => t a -> a
foldMap :: Monoid b => (a -> b) -> t a -> b
foldr :: (a -> b -> b) -> b -> t a -> b
foldl :: (a -> b -> a) -> a -> t b -> a
null :: t a -> Bool
length :: t a -> Int
elem :: Eq a => a -> t a -> Bool
maximum :: Ord a => t a -> a
minimum :: Ord a => t a -> a
sum :: Num a => t a -> a
product :: Num a => t a -> a
foldr1 :: (a -> a -> a) -> t a -> a
foldl1 :: (a -> a -> a) -> t a -> a
toList :: t a -> [a]
-- default definitions
null = null . toList
length = length . toList
elem x = elem x . toList
maximum = maximum . toList
minimum = minimum . toList
sum = sum . toList
product = product . toList
foldr f v = foldr f v . toList
foldl r v = foldl f v . toList
foldr1 f = fold1 f . toList
foldl1 f = fold1 f . toList
fold = foldMap id
foldMap f = foldr (mappend . f) mempty
toList = foldMap (\x -> [x])
List
instance Foldable [] where
-- fold :: Monoid a => [a] -> a
fold [] = mempty
fold (x : xs) = x <> fold xs
-- foldMap :: Monoid b => (a -> b) -> [a] -> b
foldMap _ [] = mempty
foldMap f (x : xs) = f x <> foldMap f xs
-- foldr :: (a -> b -> b) -> b -> [a] -> b
foldr _ v [] = v
foldr f v (x : xs) = f x (foldr f v xs)
-- foldl :: (a -> b -> a) -> a -> [b] -> a
foldl _ v [] = v
foldl f v (x : xs) = foldl f (f v x) xs
getSum (foldMap Sum [1..10]) -- 55
getProduct (foldMap Product [1..10]) -- 3628800
Tree
data Tree a = Leaf a | Node (Tree a) (Tree a)
deriving (Show)
instance Foldable Tree where
-- fold :: Monoid a => Tree a -> a
fold (Leaf x) = x
fold (Node l r) = fold l <> fold r
-- foldMap :: Monoid b => (a -> b) -> Tree a -> b
foldMap f (Leaf x) = f x
foldMap f (Node l r) = foldMap f l <> foldMap f r
-- foldr :: (a -> b -> b) -> b -> Tree a -> b
foldr f v (Leaf x) = f x v
foldr f v (Node l r) = foldr f (foldr f v r) l
-- foldl :: (a -> b -> a) -> a -> Tree b -> a
foldl f v (Leaf x) = f v x
foldl f v (Node l r) = foldl f (foldl f v l) r
tree :: Tree Int
tree = Node (Node (Leaf 1) (Leaf 2)) (Leaf 3)
foldr (+) 0 -- 1 + (2 + (3 + 0))
foldl (+) 0 -- ((0 + 1) + 2) + 3
foldl (+) (Node (Leaf 1) (Leaf 2)) -- 3
toList (Node (Leaf 1) (Leaf 2)) -- [1,2]
Generic Functions
import Data.Foldable
data Tree a = Leaf a | Node (Tree a) (Tree a)
deriving (Show)
instance Foldable Tree where
-- foldMap :: Monoid b => (a -> b) -> Tree a -> b
foldMap f (Leaf x) = f x
foldMap f (Node l r) = foldMap f l <> foldMap f r
average :: [Int] -> Int
average ns = sum ns `div` length ns
average' :: Foldable t => t Int -> Int
average' ns = sum ns `div` length ns
main = do
print (average' [1 .. 10]) -- 5
print (average' (Node (Leaf 1) (Leaf 3))) -- 2
and()
and :: Foldable t => t Bool -> Bool
and = getAll . foldMap All
main = do
print (and [True, False, True]) -- False
or()
or :: Foldable t => t Bool -> Bool
or = getAny . foldMap Any
main = do
print (or (Node (Leaf True) (Leaf False))) -- True
all()
all :: Foldable t => (a -> Bool) -> t a -> Bool
all p = getAll . foldMap (All . p)
main = do
print (all even [1, 2, 3]) -- False
any()
any :: Foldable t => (a -> Bool) -> t a -> Bool
any p = getAny . foldMap (Any . p)
main = do
print (any even (Node (Leaf 1) (Leaf 2))) -- True
concat()
concat :: Foldable t => t [a] -> [a]
concat = fold
main = do
print (concat ["ab", "cd", "ef"]) -- "abcdef"
print (concat (Node (Leaf [1, 2]) (Leaf [3]))) -- [1,2,3]
Traversable
Note:
A definition of either traverse or sequenceA is needed but traverse is prefarable rather than sequenceA because default traverse definition is unefficient due to passing through the data structure twice, when fmap and sequenceA.
class (Functor t, Foldable t) => Traversable t where
traverse :: Applicative f => (a -> f b) -> t a -> f (t b)
traverse g = sequenceA . fmap g
sequenceA :: Applicative f = t (f a) -> f (t a)
sequenceA = traverse id
mapM :: Monad m => (a -> m b) -> t a -> m (t b)
mapM = traverse
sequence :: Monad m => t (m a) -> m (t a)
sequence = sequenceA
List
instance Traversable [] where
-- traverse :: Applicative f => (a -> f b) -> [a] -> f [b]
traverse g [] = pure []
traverse g (x : xs) = pure (:) <*> g x <*> traverse g xs
dec :: Int -> Maybe Int
dec n = if n > 0 then Just (n - 1) else Nothing
main = do
print (traverse dec [1, 2, 3]) -- Just [0,1,2]
print (traverse dec [2, 1, 0]) -- Nothing
print (sequenceA [Just 1, Just 2, Just 3]) -- Just [1, 2, 3]
print (sequenceA [Just 1, Nothing, Just 3]) -- Nothing
Tree
instance Traversable Tree where
-- traverse :: Applicative f => (a -> f b) -> Tree a -> f (Tree b)
traverse g (Leaf x) = pure Leaf <*> g x
traverse g (Node l r) = pure Node <*> traverse g l <*> traverse g r
dec :: Int -> Maybe Int
dec n = if n > 0 then Just (n - 1) else Nothing
main = do
print (traverse dec (Node (Leaf 1) (Leaf 2))) -- Just (Node (Leaf 0) (Leaf 1))
print (traverse dec (Node (Leaf 0) (Leaf 1))) -- Nothing
print (sequenceA (Node (Leaf (Just 1)) (Leaf (Just 2)))) -- Just (Node (Leaf 1) (Leaf 2))
print (sequenceA (Node (Leaf (Just 1)) (Leaf Nothing))) -- Nothing
Lazy Evaluation
Lazy evaluation is the use of call-by-name evaluation in conjunction with sharing such as using pointer
In Haskell, any two different ways of evaluating the same expression will always produce the same final value, provided that they both terminate.
inc :: Int -> Int
inc n = n + 1
-- from right
inc (2 * 3)
= { applying * }
inc 6
= { applying inc }
6 + 1
= { applying + }
7
-- from left
inc (2 * 3)
= { applying inc }
(2 * 3) + 1
= { applying * }
6 + 1
= { applying + }
7
call-by-value evaluation
call-by-name evaluation is preferable to call-by-value for ensuring that evaluation terminates as often as possible.
call-by-name evaluation will terminate if there exists any evaluation sequence that terminates for a given expression, and produce the same final value.
square :: Int -> Int
square n = n * n
square (1 + 2)
= { applying square }
(1 + 2) * (1 + 2)
= { applying the first +}
3 * (1 + 2)
= { applying + } -- redundant reduction but can be resolved by using pointer to copy `(1 + 2)`
3 * 3
= { applying * }
9
the following expression terminates in call-by-name evaluation.
inf :: Int
inf = 1 + inf
fst (0, inf)
= { applying fst }
0
call-by-name evaluation
square (1 + 2)
= { applying + }
square 3
= { applying square }
3 * 3
= { applying * }
9
the following expression does not terminate in call-by-value evaluation.
fst (0, inf)
= { applying inf }
fst (0, 1 + inf)
= { applying inf }
fst (0, 1 + (1 + inf))
= { applying inf }
...
Modular Programming
Lazy evaluation allows us to separate control from data in our computations.
-- take 3: control
-- ones: data
take 3 ones -- [1,1,1]
-- pattern of without lazy evaluation:
-- need to make (= control) a certain data.
-- cannot separate control from data.
replicate 3 1 -- [1,1,1]
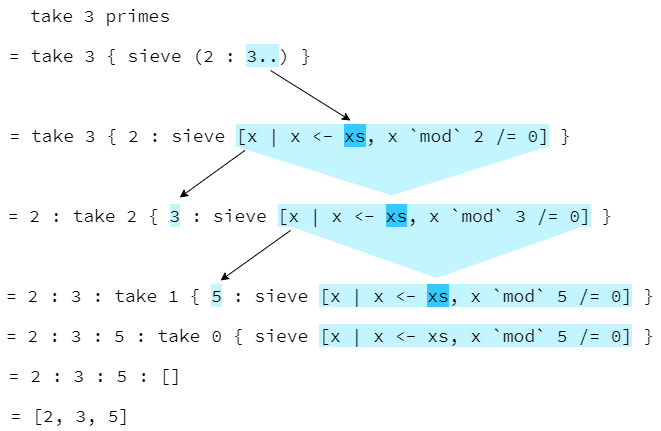
the sieve of Eratosthenes
primes :: [Int]
primes = sieve [2 ..]
sieve :: [Int] -> [Int]
sieve (p : xs) = p : sieve [x | x <- xs, x `mod` p /= 0]
main = do
print (take 10 primes) -- [2,3,5,7,11,13,17,19,23,29]
print (takeWhile (< 10) primes) -- [2,3,5,7]
Strict Application
strict functions such as built-in arithmetic operator, * and + cannot be applied until their two arguments have been evaluated to numbers; values
f $! x; f is immediately applied to x (if x is an expression, after evaluation of x)
$! serves as a stopper for outmost evaluation
square $! (1 + 2)
= { applying + }
square $! 3
= { applying $! }
square 3
= { applying square }
3 * 3
= { applying * }
9
strict application is mainly used to improve the space performance of programs.
pattern with lazy evaluation
sumwith :: Int -> [Int] -> Int
sumwith v [] = v
sumwith v (x : xs) = sumwith (v + x) xs
sumwith 0 [1, 2, 3]
= { applying sumwith }
sumwith (0 + 1) [2, 3]
= { applying sumwith }
sumwith ((0 + 1) + 2) [3]
= { applying sumwith }
sumwith (((0 + 1) + 2) + 3) []
= { applying sumwith }
((0 + 1) + 2) + 3 -- the length is the same with the original list so sumwith requires much space for evaluation if given a long list.
= { applying the first + }
(1 + 2) + 3
= { applying the first + }
3 + 3
= { applying + }
6
pattern with strict application
sumwith :: Int -> [Int] -> Int
sumwith v [] = v
sumwith v (x : xs) = (sumwith $! (v + x)) xs
sumwith 0 [1, 2, 3]
= { applying sumwith }
(sumwith $! (0 + 1)) [2, 3]
= { applying + }
(sumwith $! 1) [2, 3]
= { applying $! }
sumwith 1 [2, 3]
= { applying sumwith }
(sumwith $! (1 + 2)) [3]
= { applying + }
(sumwith $! 3) [3]
= { applying $! }
sumwith 3 [3]
= { applying sumwith }
(sumwith $! (3 + 3)) []
= { applying + }
(sumwith $! 6) []
= { applying $! }
sumwith 6 []
= { applying sumwith }
6
foldl'
-- in Data.Foldable
foldl' :: (a -> b -> a) -> a -> [b] -> a
foldl' f v [] = v
foldl' f v (x : xs) = ((foldl' f) $! (f v x)) xs
Reasoning
Induction
can be used to confirm the logic or propeties of a recursive type or a recursive function is correct.
e.g.1 (about natural number)
replicate :: Int -> a -> [a]
replicate 0 _ = []
replicate n x = x : replicate (n - 1) x
-- hypothesis:
-- replication function produce a list when n elements, that is `length (replicate n x) = n`
-- Base case:
length (replicate 0 x)
= { applying replicate }
length []
= 0
-- Inductive case
length (replicate (n + 1) x)
= { applying replicate }
length (x : replicate n x)
= { applying length }
1 + length (replicate n x)
= { induction hypothesis }
1 + n
= { commutativity of + }
n + 1
e.g.2 (about list)
reverse :: [a] -> [a]
reverse [] = []
reverse (x : xs) = reverse xs ++ x
-- hypothesis 1:
-- contravariant; reverse (xs ++ ys) = reverse ys ++ reverse xs
-- Base case:
reverse ([] ++ ys)
= { applying ++ }
reverse ys
= { identity for ++ }
reverse ys ++ []
= { unapplying reverse }
reverse ys ++ reverse []
-- Inductive case:
reverse ((x : xs) ++ ys)
= { applying ++ }
reverse (x : (xs ++ ys))
= { applying reverse }
reverse (xs ++ ys) ++ [x]
= { induction hypothesis }
(reverse ys ++ reverse xs) ++ [x]
= { associativity of ++ }
reverse ys ++ (reverse xs ++ [x])
= { unapplying the second reverse }
reverse ys ++ reverse (x : xs)
-- hypothesis 2:
-- reverse (reverse (x : xs)) = x : xs
-- Base case:
reverse (reverse [])
= { applying the inner reverse }
reverse []
= { appyling reverse }
[]
-- Inductive case:
reverse (reverse (x : xs))
= { applying the inner reverse }
reverse (reverse xs ++ [x])
= { contravariant }
reverse [x] ++ reverse (reverse xs)
= { singleton lists }
[x] ++ reverse (reverse xs)
= { induction hypothesis }
[x] ++ xs
= { applying ++ }
x : xs
e.g.3 (about fmap low on list)
fmap id = id
fmap (g . h) = fmap g . fmap h
fmap :: (a -> b) -> [a] -> [b]
fmap g [] = []
fmap g (x : xs) = g x : fmap g xs
-- hypothesis 1: fmap id = id
-- Base case:
fmap id []
= { applying fmap }
[]
-- Inductive case:
fmap id (x : xs)
= { applying fmap }
id x : fmap id xs
= { applying id }
x : fmap id xs
= { induction hypothesis }
x : xs
-- hypothesis 2:
-- fmap (g . h) = fmap g . fmap h
-- i.e. fmap (g . h) xs = fmap g (fmap h xs)
-- Base case:
fmap (g . h) []
= { applying fmap }
[]
= { unapplying fmap }
fmap g []
= { unapplying fmap }
fmap g (fmap h [])
-- Inductive case:
fmap (g . h) (x : xs)
= { applying fmap }
(g . h) x : fmap (g . h) xs
= { applying . }
g (h x) : fmap (g . h) xs
= { induction hypothesis }
g (h x) : fmap g (fmap h xs)
= { unapplying fmap }
fmap g (h x : fmap h xs)
= { unapplying fmap }
fmap g (fmap h (x : xs))
Improve Computing Time
reverse()
reverse function run by because in general xs ++ ys needs (length xs) + 1 steps to concatinate xs and xs, so reverse xs ++ [x] is bottle neck.
we try to difine another version reverse; reverse' to improve computing time.
reverse :: [a] -> [a]
reverse [] = []
reverse (x : xs) = reverse xs ++ [x]
-- hypothesis to construct the definition of reverse':
-- reverse' xs ys = xs ++ ys
-- Base case:
reverse' [] ys
= { specification of reverse' }
reverse [] ++ ys
= { applying reverse }
[] ++ ys
= { applying ++ }
ys
-- Inductive case:
reverse' (x : xs) ys
= { specification of reverse' }
reveres (x : xs) ++ ys
= { applying reverse }
(reverse xs ++ [x]) ++ ys
= { associativity of ++ }
reverse xs ++ ([x] ++ ys)
= { induction hypothesis }
reverse' xs ([x] ++ ys)
= { applying ++ }
reverse' xs (x : ys)
we obtain another definition of reverse' .
reverse' :: [a] -> [a] -> [a]
reverse' [] ys = ys
reverse' (x : xs) ys = reverse' xs (x : ys)
reverse :: [a] -> [a]
reverse xs = reverse' xs [] -- = foldl (\xs x -> x : xs) []
reverse [1, 2, 3]
= { applying reverse }
reverse' [1, 2, 3] []
= { applying reverse' }
reverse' [2, 3] (1 : [])
= { applying reverse' }
reverse' [3] (2 : (1 : []))
= { applying reverse' }
reverse' [] (3 : (2 : 1 : []))
= { applying reverse' }
3 : (2 : 1 : [])
flatten()
data Tree = Leaf Inf | Node Tree Tree
flatten :: Tree -> [Int]
flatten (Leaf n) = [n]
flatten (Node l r) = flatten l ++ flatten r
-- hypothesis to construct an improved definition of flatten; flatten'
-- flatten' t ns = flatten t ++ ns
-- Base case:
flatten' (Leaf n) ns
= { specification of flatten' }
flatten (Leaf n) ++ ns
= { applying flatten }
[n] ++ ns
= { applying ++ }
n : ns
-- Inductive case:
flatten' (Node l r) ns
= { specification of flatten' }
flatten (Node l r) ++ ns
= { applying flatten }
(flatten l ++ flatten r) ++ ns
= { associativity of }
flatten l ++ (flatten r ++ ns)
= { induction hypothesis for l }
flatten' l (flatten r ++ ns)
= { induction hypothesis for r }
flatten' l (flatten' r ns)
we obtain the following definition.
flatten' :: Tree -> [Int] -> [Int]
flatten' (Leaf n) ns = n : ns
flatten' (Node l r) ns = flatten' l (flatten' r ns)
flatten :: Tree -> [Int]
flatten t = flatten' t []